NERD ALERT!

(for all your super-duper techie stuff)

One of the most frequent ‘problems’ that I hear about when talking about compensated lenses is when we’re dealing with spheres. All too frequent are exchanges like this:

• Doctor:    I ordered this lens as a sphere, but there’s cylinder in it – it’s wrong!
• Lab:    Yes, I understand you ordered it as a sphere, but the lens is compensated, so…
• Doctor:    I know how compensation works, I’ve been doing this for thirty years. But I ordered a sphere, so it shouldn’t have any cylinder.

Well, here’s what’s up, Doc: using conventional lenses, you’d be right. We’re not using conventional lenses, these lenses are compensated. This hasn’t really been “a thing” until recent years. Up until recently, “prescription changes due to the position of wear, particularly those associated with lens tilt, have been largely ignored in the past.” (Meister, 20131) In the past, technology just wasn’t at a level to be able to do the computations necessary to create a lens, and then actually make it. Now, of course, we can build them…we have the technology.

Now that we can compensate, of course, it’s important to understand why it is we are doing the compensation. We do this because we are trying to make the best lens for the patient – not the best lens for the lensometer. When you check the power in the lensometer, you’re replicating the exact same conditions of the phoropter in the exam. You are checking one specific point at a 90 degree angle to the lens. While that makes checking the lens easy, it doesn’t result in the best possible lens for the patient. We need to account for how light works and bends when it hits the lens. This means accounting for the differences between refraction and the actual frame the patient picks out. When we refract, the lenses in the phoropter are completely straight – no wrap, tilt, or curves. The distance between the eye and the lenses is also different when we compare refraction to real frames. When the patient picks out a frame, there’s always going to be some degree of tilt and wrap. So that means we have to make a lens to bend the light so that what actually enters the eye is the correct prescription, even if that means the lens prescription is different.

Now, actual lens compensation is fairly complex and take a lot of things into account, such as lens thickness, prism, cylinder, and basically anything else you can think of. However, to understand the basic idea, we can use Coddington’s equations (Keating, 20022) as an example. What these equations will do is account for the prescription compensation along a single axis of tilt. It doesn’t take into account all of the other factors used in lens compensation, since this is a magazine, not a textbook.

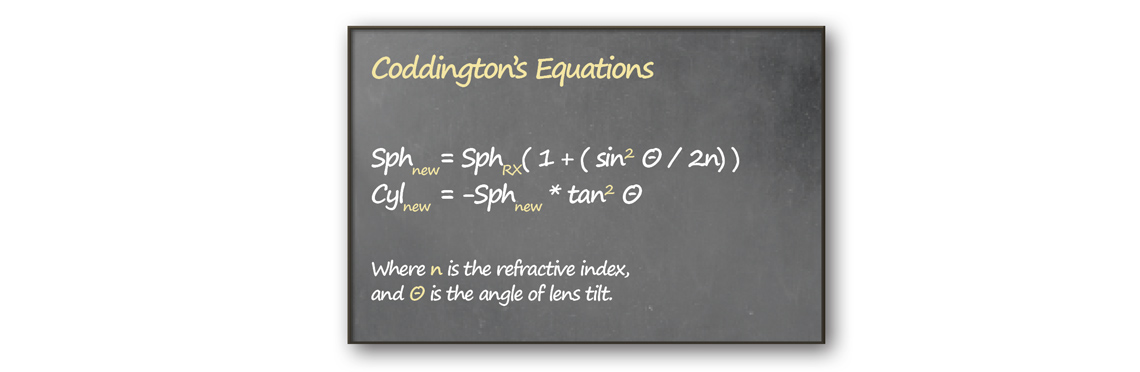
So, as an example let’s say we have done a refraction of a -5.00 sphere. If we do the above calculation, we should come out with the exact same numbers, since our compensation is effectively nothing. I’ll use 1.523 for the refractive index, assuming the lenses in the phoropter are glass.

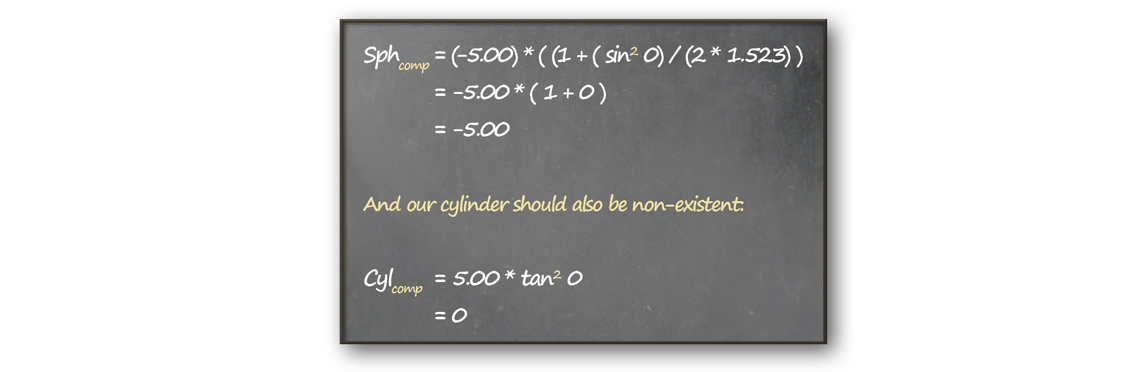
So this is exactly what we’d expect – we don’t have to compensate since there’s no difference between the position of the starting lens and the ending lens. So now that we have the basic idea down, let’s try the same lens, but this time in a different frame. This time we’ll assume it’s going to be a wrap sunglass frame, having an angle of 20 degrees. We’ll assume it’s still glass, just to keep our number consistent.

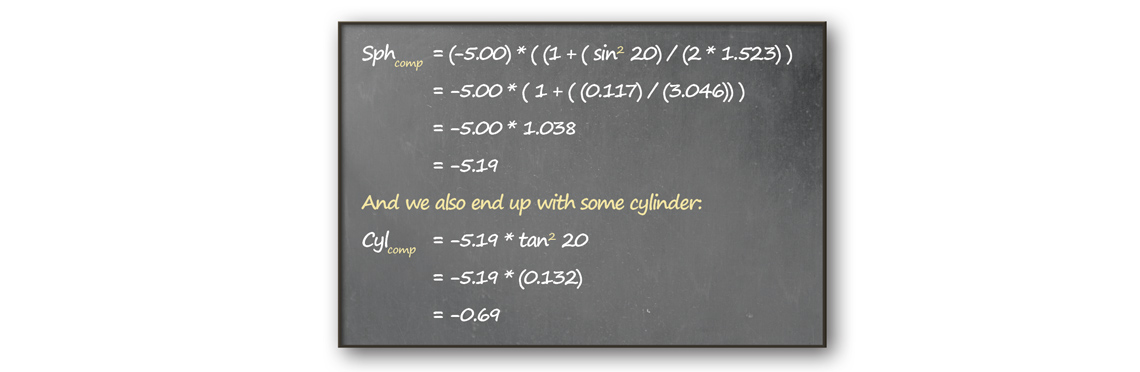
With this much of an angle, we get a sphere of -5.19 and a cylinder of -0.69. To find the axis, we go off of the way in which the lens was tilted. 90 degrees for a frame-wrap type tilt, and 180 degrees for a pantoscopic type tilt (Keating, 19953) . Obviously, this is a simple calculation. Real-life lenses have multiple type of tilt to them, so would have more complex equations to take all of the factors in to account.

Another thing to keep in mind is that the higher the prescription, the larger the amount of compensation is going to be. To take a look at that, we can use a much higher prescription (-12.00) with the same angle, still in glass for the sake of consistency:

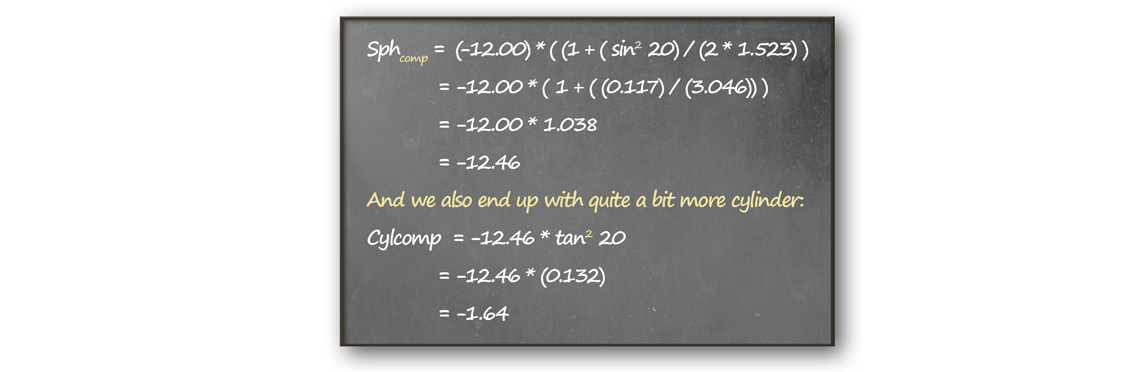
So now, our prescription not only has almost a half diopter of additional power in the sphere, but also over a diopter and a half of cylinder. By turning the lens at this 20 degree angle, we end up inducing a lot of cylinder that we need to basically undo before the light gets to the patient’s eye. Again, if these lenses were straight, they’d perfectly match the refracted prescription.

Obviously, this isn’t something that you are ever going to need to calculate yourself. When it comes to real-world compensation, there’s far too many things to make a calculation by hand. What this does do, however, is give you an idea of exactly how much the prescription can be influenced by the position of the lens. The larger the tilt or wrap, the more cylinder that gets induced and the more different from the refracted prescription you will be.

Lewis Skolnick

Try it out:

Take any stock lens – even a plano. Hold it in front of your eye and focus on something in the distance. Slowly turn it to simulate a high wrap frame – one edge turns towards you and the other away from you. As you turn it, you can notice the power change as the image you are looking at will blur.

Sources:

1. Meister, D. Memorandum to the Vision Council Technical Committee, Understanding the Position of Wear. January 11, 2013.
2. Keating, M. Oblique central refraction in spherocylindrical corrections with both faceform and pantoscopic tilt. Optometry & Vision Science 1995;72:258-265.
3. Keating M. Geometric, Physical, and Visual Optics. 2nd edition. Boston: Butterworth-Heinemann; 2002:457-460.